The Poisson process is a mathematical abstraction of random events happening over a stretch of time. It’s often used to model all sorts of occurrences from particle emission due to radioactive decay, to natural disasters.¹ The process itself has several mathematical properties such as not allowing for simultaneous events, but these specifics aren’t important for our purposes. What makes it useful to software engineers is that it also turns out to be a good model for events like hits to a webpage² or requests to an API. For example, suppose you have written a new API for your web site, and you wanted to test it out under normal load. In order to simulate this with a Poisson process, all you’d need to know is the expected number of hits per hour (or minute or second). With this information, you could then generate random inter-arrival times (the times between events). That is, you could model the amount of time between requests to your API using this equation:³

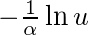
This is the equation for an exponentially distributed random variable, where U is a random number between 0 and 1, and 1/α is the expected value of the inter-arrival times. In English, this means that if you expect 100 hits per hours, then 1/α would equal 1/100 (because you expect there to be a hit every 0.01 hours), and U would be some random number generated with a call to Math.random(). The number that pops out the other end would be a randomly generated inter-request time. If you wanted to simulate more than one request, you would evaluate this equation multiple times (using a new randomly generated U each time), and each result would be the time between two requests. So if you ended up with 0.04, 0.2, 0.1, then the second request would come in 0.04 hours after the first, and the third would come in 0.2 hours after the second, and so on.

This technique can be automated using a simple Python script:

1
2
3
4
5
6
7
8
9
10
11
12

# Make a function iterable, by repeatedly calling it.
def make_iterable(func, *args):
    try:
        while 1:
            yield func(*args)
    except:
        pass

uni_rand = make_iterable(random.uniform, 0, 1)

# A generator for inter arrival times.
inter_arrival = ( -(1./a)*math.log(u) for u in uni_rand)

This creates a generator inter_arrival which generates one inter-arrival time every time it’s iterated on. Using this to test an API is as simple as:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

import random
import math
import sys
import time

# Expected number of arrivals per unit time.
a = float(sys.argv[1])
# Number of events
count = int(sys.argv[2])

# Function for testing API
def test_api():
    print "Testing API..."
    # TODO: Make request to the API

# Make a function iterable, by repeatedly calling it.
def make_iterable(func, *args):
    try:
        while 1:
            yield func(*args)
    except:
        pass

uni_rand = make_iterable(random.uniform, 0, 1)

# A generator for inter-arrival times.
inter_arrival = ( -(1./a)*math.log(u) for u in uni_rand)

# Generate inter-arrival times, then sleep for that long.
inter_arrival_iter = iter(inter_arrival)
for i in xrange(count):
    inter_arrival_seconds = inter_arrival_iter.next() * 3600.
    print "Sleeping for %f seconds." % inter_arrival_seconds
    time.sleep(inter_arrival_seconds)
    test_api()

This script takes in two arguments. The first is the expected number of events per hour, and the second is the number of events to generate. The last loop is where the testing occurs. It generates one inter-arrival time, sleeps for that long, and then calls the test_api function which would need to be filled in with the API test.

Running this file with input 3600 10 generates 10 events, each one spaced by about 1 second:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

% python poisson.py 3600 10
Sleeping for 1.710953 seconds.
Testing API...
Sleeping for 5.028327 seconds.
Testing API...
Sleeping for 0.511307 seconds.
Testing API...
Sleeping for 2.336480 seconds.
Testing API...
Sleeping for 1.594504 seconds.
Testing API...
Sleeping for 0.308939 seconds.
Testing API...
Sleeping for 0.682607 seconds.
Testing API...
[snip]

References

1. Tijms, Henk. Understanding Probability: Chance Rules in Everyday Life. 2nd ed. New York: Cambridge University Press, 2010. 118. Print.
2. Arlitt, Martin F.; Williamson, Carey L. (1997). “Internet Web servers: Workload characterization and performance implications”. IEEE/ACM Transactions on Networking 5 (5): 631. DOI:10.1109/90.649565
3. Ibid 1. Page 124